Функции Грина

Функции Грина – это альтернативный способ решать неоднородные задачи с неоднородными краевыми условиями.

Дана область с границей . - функции от .

Оператор

Вторая формула Грина

-непрерывные функции с непрерывными первыми и вторыми производными вплоть до границы

Теорема о среднем арифметическом: Значение гармонической функции в центре шара равно среднему арифметическому ее значений на поверхности шара.

Доказательство:

Пусть гармоническая функция внутри шара.

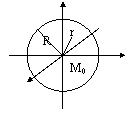
Пусть , - центр шара, - радиус шара. - поверхность шара.

Применим формулу интегрального представления функций класса и учтем предположение о том, что функция гармоническая ( в ).

. В данном

случае

Для гармонической функции по замкнутой области интеграл равен 0

. Теорема доказана.

На основе теоремы о среднем арифметическом докажем теорему о максимуме (минимуме).

Теорема о максимуме (минимуме):

Функция, гармоническая внутри ограниченной области и непрерывная в замкнутой области с границей , достигает наибольшее (наименьшее) значение только на границе области, кроме того случая, когда эта функция константа.

Доказательство: от противного(?).

Пусть достигает максимума в точке Проведем сферу с центром в точке таким образом, чтобы она целиком принадлежала . Применим теорему о среднем арифметическом гармонической функции к сфере и заменим подынтегральную функцию ее наибольшим значением :

Вместо неравенства будет равенство, поскольку - наибольшее значение в области можем утверждать, что во всякой сфере, принадлежащей c центром в точке во всей области . Докажем это:

Пусть - произвольная точка, покажем, что . Соединим и кривой , - кратчайшее расстояние в области от любой точки, принадлежащей , до любой точки поверхности, ограничивающей область .