1. Методы одномерного поиска

1. Метод дихотомии.

Точки 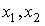выбираются на расстоянии 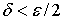от середины отрезка:

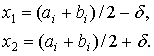 (1)        

И в каждой из найденных точек вычисляем значения функци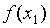и: и .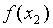

Далее сокращаем интервал неопределенности и получаем интервал 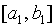следующим образом.

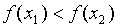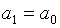Если , то и .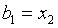

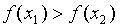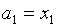В противном случае, если , то и .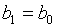

За одну итерацию интервал неопределенности уменьшается примерно в два раза (рис. 1). За 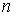итераций длина интервала будет примерно равна 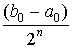. Для достижения точности 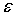потребуется 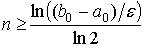итераций. На каждой итерации минимизируемая функция вычисляется дважды.

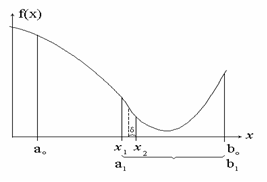
Рис. 1. Метод дихотомии

Поиск заканчивается, если длина интервала неопределенности 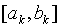  на текущей итерации становится меньше заданной точности: .

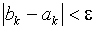2. Метод золотого сечения.

Точки 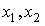находятся симметрично относительно середины отрезка 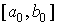и делят его в пропорции золотого сечения, когда длина всего отрезка относится к длине большей его части также, как длина большей части относится к длине меньшей част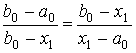и:

и .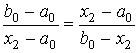

Отсюда

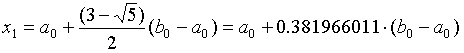
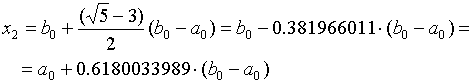              (2)

Сокращаем интервал неопределенности.

1) Если 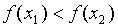, то , , .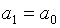

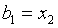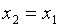2) В противном случае, если 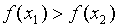, то , , .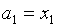

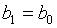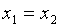На последующих итерациях производим расчет только той точки и ее функции, которую необходимо обновить.

Поиск прекращается при выполнении .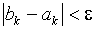

Для достижения точности 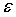потребуется 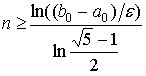итераций.

      Неточное задание величины 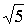на ЭВМ уже при достаточно небольшом количестве итераций может приводить к погрешностям и потере точки минимума, так как она выпадает из интервала неопреде­ленности. Поэтому, вообще говоря, при реализации алгоритма возможность такой ситуации должна быть предусмотрена.

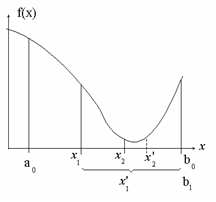
Метод золотого сечения

3. Метод Фибоначчи.

Числа Фибоначчи подчиняются соотношениям:

,

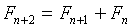где 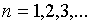и .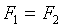

С помощью индукции можно показать, что 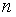-е число Фибоначчи вычисляется по формуле:

,

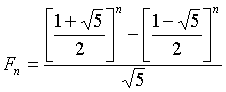где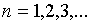

Из данной формулы видно, что при больших значениях 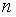выполняется соотношение:

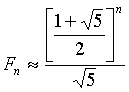,так, что числа Фибоначчи с увеличением 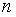растут очень быстро.

На начальном интервале вычисляют точки

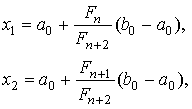                                      (3)

где 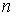выбирается исходя из точности и начальной длины интервала (см. ниже соотношение (5)).

Интервал неопределенности сокращается точно так же, как в методе золотого сечения. И на новой итерации вычисляется только 1 новая точка и значение функции в ней.

На 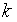-й итерации получаем точку минимума, которая совпадает с одной из точек, которые вычисляются по формулам

,

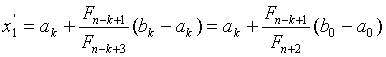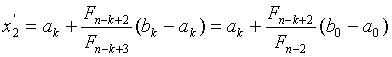
и расположены на отрезке 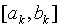симметрично относительно его середины.

Нетрудно заметить, что при 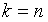точк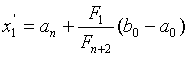и:

 и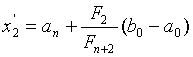  

совпадают и делят отрезок 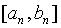пополам.

Следовательно, .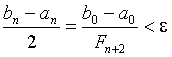

Отсюда можно выбрать 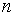из условия .

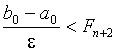Таким образом, это условие позволяет до начала работы алгоритма определить число итераций, необходимое для определения минимума с точностью 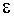при начальной величине интервала .

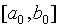С ростом 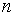из-за того, что 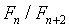- бесконечная десятичная дробь, возможно “искажение” метода и потеря интервала с точкой минимума (вследствие погрешностей вычислений).

Следует также отметить, что при практическом применении метод золотого сечения по эффективности, скорости сходимости и точности получаемого решения практически не уступает методу Фибоначчи. А алгоритмически реализация метода золотого сечения является более простой.

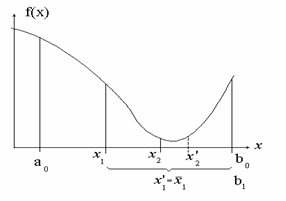
Рис. 3. Метод Фибоначчи

4. Метод квадратичной интерполяции (метод парабол)

Идея метода заключается в следующем:

Если на отрезке [a,b] с внутренней точкой x*=arg min{φ(x): xÎ[a,b]} функция φ(х) достаточно хорошо аппроксимируется многочленом второй степени, то за приближенное значение х* целесообразно взять точку минимума этого многочлена.

Метод целесообразно применять после того, как найден отрезок достаточно малой длинны, содержащий x*, например, после того как найдены [ak,bk] и xk в результате k шагов по золотого сечения.

Пусть известна удачная тройка чисел х1, х2 и х3 (x1<x2<x3, φ2<=min{φ1,φ3} φ2<max{φ1,φ3}), т.о. отрезку [x1,x3] обязательно принадлежит точка минимума.

Многочлен второго порядка, график которого проходит через точки (х1,φ1), (х2,φ2) и (х3,φ3) достигает минимального значения в точке

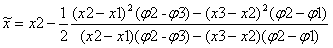
Схема:

      Имеем х1, х2, х3 и соответствующие φ1, φ2, φ3 и задана точность e определения интервала, содержащего точку х*.

      Шаг 1. Вычислим .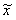

      Шаг 2. Если |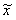-x2|<=e, закончить поиск, положив х*~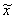. Если |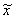-x2|>e, то вычислить φ().

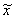      Шаг 3. Из чисел х1, х2, х3 и 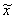выбираем удачную тройку чисел и переходим на 1.

Выбираем удачную тройку:

      Имеем (х1, φ1), (x2, φ2), (x3, φ3) и (x4, φ4), такие что

x1<x2<x3<x4, φ<=min{ φ1, φ4}, φ3<=min{ φ1, φ4}

При φ2< φ3 удачная тройка х1, х2, х3.

При φ2> φ3 удачная тройка х1, х2, х4.

При φ1= φ3 – обе удачные.