Одношаговые явные схемы. Чехарда со средних точек.

Схема (5) имеет второй порядок аппроксимации и по времени и пространству. Это означает, что вычисление значения на n+1 слое возможно при известных значениях на n и  n-1 слое.

 

 

Необходимо отметить, что каждое новое значение U на четном временном слое вычисляется через значение на предыдущем четном временном слое. А предыдущий нечетный временной слой «перекрывается».

Метод Фон Неймана   

Каждую компоненту представим Фурье образом

Подставим (11) в (9), получим:

 

Из (12) и (13) выпишем систему уравнений

 

Условие устойчивости определяется следующим:

 

Абсолютная величина  будет больше 1 - это означает неустойчивость схемы (5)

   - условие устойчивости

 

Произвольное начальное приближение сдвигается со скоростью конвекции, равной а. Это означает, что

Таким образом, метод Фон Неймана показывает, что схема Чехарда правильно моделирует одно из главных свойств, присущих уравнению (1), а именно, отсутствие затухания.

Рассмотрим устойчивость разностной схемы стационарной задачи

Сеточная функция

Предположим, что (1) однозначно разрешима =>

Введем в рассмотрение скалярное произведение (y,V) и порожденную им норму

, тогда решение задачи (1) будет удовлетворять

 

 - априорные оценки

 

Из этих тождественных соотношений можно получить норму решения у через правую часть (1)

Пусть оператор А положительно определен => из (2) и из неравенства Коши-Буняковского

 

    => 

 

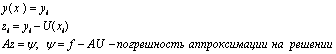
Пусть задача устойчива, тогда справедливо следующее:

Оценка (7) свидетельствует о том, что имеет место сходимость нашей задачи тогда и только тогда, когда  при

Необходимо доказать устойчивость и проверить стремление к нулю