Основные уравнения математической физики

Уравнения колебаний

(1)

Коэффициенты определяются свойствами среды. - постоянно действующий внешний фактор. В соответствии с определением в декартовых координатах . Этот оператор эллиптический. В целом задача гиперболическая.

Вывод уравнения (1) на примере малых поперечных колебаний струны.

Струной называется натянутая нить, не сопротивляющаяся изгибу. Пусть в плоскости струна совершает малые поперечные колебания (т.е. около своего положения равновесия). Тогда величина отклонения в точке в момент времени обозначим . Ограничимся рассмотрением малых колебаний струны , т.е. будем пренебрегать величинами высших порядков малости по сравнению с .

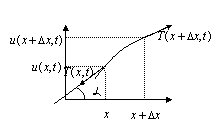
Т.к. струна не сопротивляется изгибу, то ее натяжение в точке в момент времени направлено по касательной в этой точке. Любой участок струны после отклонения от положения равновесия в рамках введенных ограничений не изменит своей длины.

В соответствии с законом Гука величина натяжения будет величиной постоянной, не зависящей от и .

Пусть - плотность внешних сил, действующих на струну в точке в момент времени . Причем эти силы направлены перпендикулярно в плоскости . Пусть - линейная плотность материала, из которого сделана струна. - масса элемента струны длиной . На элемент струны длиной действует сила натяжения равная . На этот элемент действует внешняя сила, а их сумма по закону Ньютона равна массе элемента, умноженной на ускорение.